How to draw the Euler angles in the xy plane for head pose

When I drew the head pose on the xy plane, I had no idea how to draw it. This article is just a summary.

Head pose visualization

Head pose is a representation of the human head orientation.
To visualise head pose, this article draws the xyz unit vector on an image of a human head.
X-axis is drawn in red
Y-axis is drawn in green
Z-axis (out of the screen) is drawn in blue

From: Towards Robust and Unconstrained Full Range of Rotation Head Pose Estimation

The Euler angles for head pose

The definition of the Euler angles for head pose is shown in the following left figure.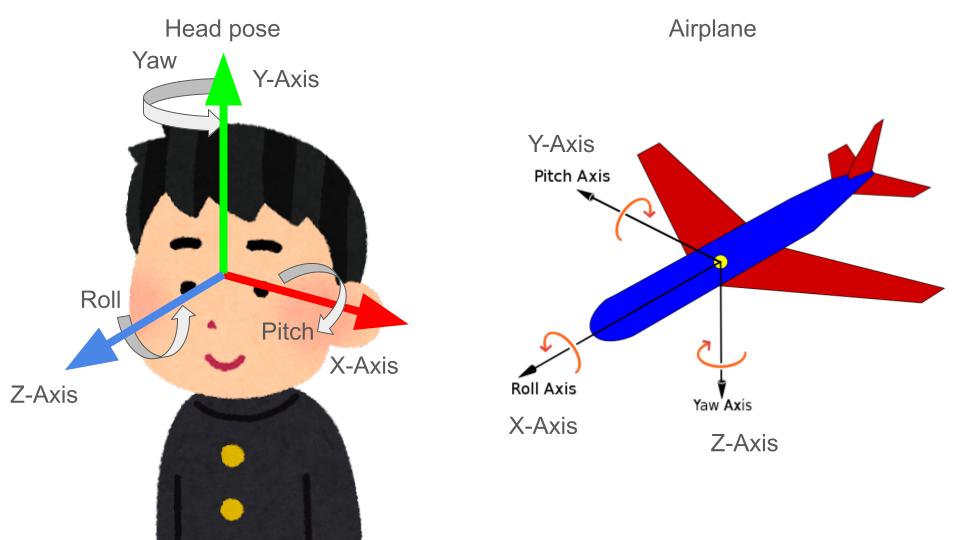

From: Aircraft principal axes

The representation of roll, pitch and yaw in xyz space depends on a perspective (field).
For example, a roll from the airplane's perspective rotates around the X-axis, but a roll from the head pose's perspective rotates around the Z-axis.

1. Convert the Euler angles to the rotation matrix

From this chapter, I explain how to draw the Euler angles in the xy plane.
First of all, convert the Euler angles to rotation matirx.
The following three basic rotation matrices rotate vectors by the Euler angles using the right-hand rule.
The rotation matrix of the X-axis is represented by $\boldsymbol{R_x}$, the rotation matrix of the Y-axis by $\boldsymbol{R_y}$ and the rotation matrix of the Z-axis by $\boldsymbol{R_z}$.

\begin{eqnarray} \boldsymbol{R_x} &=& \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos\theta_{x} & -\sin\theta_{x} \\ 0 & \sin\theta_{x} & \cos\theta_{x} \end{array} \right) \\ \end{eqnarray}

\begin{eqnarray} \boldsymbol{R_y} &=& \left( \begin{array}{ccc} \cos\theta_{y} & 0 & \sin\theta_{y} \\ 0 & 1 & 0 \\ -\sin\theta_{y} & 0 & \cos\theta_{y} \end{array} \right) \\ \end{eqnarray}

\begin{eqnarray} \boldsymbol{R_z} &=& \left( \begin{array}{ccc} \cos\theta_{z} & -\sin\theta_{z} & 0 \\ \sin\theta_{z} & \cos\theta_{z} & 0 \\ 0 & 0 & 1 \end{array} \right) \end{eqnarray}

Note:
Please replace $\theta_{x}$, $\theta_{y}$ and $\theta_{z}$ to the Euler angles.
e.g. $\theta_{x}$ means $\theta_{pitch}$ for head pose.

This article rotates in the order Z, Y, X (roll, yaw, pitch).
Note that the order of rotation affects the final result.

\begin{eqnarray} \boldsymbol{R_{zyx}} = \boldsymbol{R_x}\boldsymbol{R_y}\boldsymbol{R_z} = \left( \begin{array}{ccc} \cos\theta_{y}\cos\theta_{z} & -\cos\theta_{y}\sin\theta_{z} & \sin\theta_{y} \\ \sin\theta_{x}\sin\theta_{y}\cos\theta_{z} + \cos\theta_{x}\sin\theta_{z} & -\sin\theta_{x}\sin\theta_{y}\sin\theta_{z} + \cos\theta_{x}\cos\theta_{z} & -\sin\theta_{x}\cos\theta_{y} \\ -\cos\theta_{x}\sin\theta_{y}\cos\theta_{z} + \sin\theta_{x}\sin\theta_{z} & \cos\theta_{x}\sin\theta_{y}\sin\theta_{z} + \sin\theta_{x}\cos\theta_{z} & \cos\theta_{x}\cos\theta_{y} \end{array} \right) \end{eqnarray}

Wolfram Alpha : rotate in the order Z, Y, X

The following equations use roll, pitch and yaw notation.

\begin{eqnarray} \boldsymbol{R_{xyz}} = \left( \begin{array}{ccc} \cos\theta_{yaw}\cos\theta_{roll} & -\cos\theta_{yaw}\sin\theta_{roll} & \sin\theta_{yaw} \\ \sin\theta_{pitch}\sin\theta_{yaw}\cos\theta_{roll} + \cos\theta_{pitch}\sin\theta_{roll} & -\sin\theta_{pitch}\sin\theta_{yaw}\sin\theta_{roll} + \cos\theta_{pitch}\cos\theta_{roll} & -\sin\theta_{pitch}\cos\theta_{yaw} \\ -\cos\theta_{pitch}\sin\theta_{yaw}\cos\theta_{roll} + \sin\theta_{pitch}\sin\theta_{roll} & \cos\theta_{pitch}\sin\theta_{yaw}\sin\theta_{roll} + \sin\theta_{pitch}\cos\theta_{roll} & \cos\theta_{pitch}\cos\theta_{yaw} \end{array} \right) \end{eqnarray}

2. Project the xyz unit vector onto the xy plane

Next, to visualize the Euler angles, I draw the xyz unit vector in the xy plane (an image) as explained above.
The xyz unit vectors are represented as follows.

\begin{eqnarray} \boldsymbol{e_{x}} = \left( \begin{array}{c} 1 \\ 0 \\ 0 \end{array} \right) \boldsymbol{e_{y}} = \left( \begin{array}{c} 0 \\ 1 \\ 0 \end{array} \right) \boldsymbol{e_{z}} = \left( \begin{array}{c} 0 \\ 0 \\ 1 \end{array} \right) \end{eqnarray}

To project the xyz unit vector onto the xy plane, multiply the rotation matrix as follows

\begin{eqnarray} \widehat{\boldsymbol{e_{x}}} = \left( \begin{array}{rcc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{array} \right) \boldsymbol{R_{x}} \boldsymbol{R_{y}} \boldsymbol{R_{z}} \boldsymbol{e_{x}} = \left( \begin{array}{c} \cos\theta_{y}\cos\theta_{z} \\ \sin\theta_{x}\sin\theta_{y}\cos\theta_{z} + \cos\theta_{x}\sin\theta_{z} \\ 0 \end{array} \right) \\ \widehat{\boldsymbol{e_{y}}} = \left( \begin{array}{rcc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{array} \right) \boldsymbol{R_{x}} \boldsymbol{R_{y}} \boldsymbol{R_{z}} \boldsymbol{e_{y}} = \left( \begin{array}{c} -\cos\theta_{y}\sin\theta_{z} \\ -\sin\theta_{x}\sin\theta_{y}\sin\theta_{z} + \cos\theta_{x}\cos\theta_{z} \\ 0 \end{array} \right) \\ \widehat{\boldsymbol{e_{z}}} = \left( \begin{array}{rcc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{array} \right) \boldsymbol{R_{x}} \boldsymbol{R_{y}} \boldsymbol{R_{z}} \boldsymbol{e_{z}} = \left( \begin{array}{c} \sin\theta_{y} \\ -\sin\theta_{x}\cos\theta_{y} \\ 0 \end{array} \right) \\ \end{eqnarray}

The Euler angles can be represented on the image by drawing the XY elements of the above equation (7) ~ (8) in the xy plane.

Sample code (AFLW2000)

Example of command line:

python3 view.py --dataset_root <path/to/the/AFLW2000/root/directory> --filename image00078

Example of execution:

Sample code (view.py):

 1import os
 2import argparse
 3import cv2
 4import numpy as np
 5import scipy.io as sio
 6from math import cos, sin
 7
 8def parse_args():
 9    parser = argparse.ArgumentParser()
10    parser.add_argument('--datasets_root',
11                        help='Path to the root directory of AFLW2000 datasets',
12                        type=str)
13    parser.add_argument('--filename',
14                        help='Filename without extension to load the data',
15                        type=str)
16    args = parser.parse_args()
17    return args
18
19
20def get_R(x,y,z):
21    ''' Get rotation matrix from three rotation angles (radians). right-handed.
22    Args:
23        angles: [3,]. x, y, z angles
24    Returns:
25        R: [3, 3]. rotation matrix.
26    '''
27    # x
28    Rx = np.array([[1, 0, 0],
29                   [0, np.cos(x), -np.sin(x)],
30                   [0, np.sin(x), np.cos(x)]])
31    # y
32    Ry = np.array([[np.cos(y), 0, np.sin(y)],
33                   [0, 1, 0],
34                   [-np.sin(y), 0, np.cos(y)]])
35    # z
36    Rz = np.array([[np.cos(z), -np.sin(z), 0],
37                   [np.sin(z), np.cos(z), 0],
38                   [0, 0, 1]])
39
40    R = Rx.dot(Ry.dot(Rz))
41    return R
42
43
44if __name__ == "__main__":
45    args = parse_args()
46
47    image_file = os.path.join(args.datasets_root, '{}.jpg'.format(args.filename))
48    mat_file = os.path.join(args.datasets_root, '{}.mat'.format(args.filename))
49
50    # Load .jpg
51    img = cv2.imread(image_file)
52    # Load .mat
53    mat = sio.loadmat(mat_file)
54
55    # [pitch yaw roll tdx tdy tdz scale_factor]
56    pre_pose_params = mat['Pose_Para'][0]
57    # Get [pitch, yaw, roll]
58    pitch, yaw, roll = pre_pose_params[:3]
59
60    # Covert to R
61    x = pitch
62    y = -yaw
63    z = roll
64    R = get_R(x, y, z)
65    print("Rotation matrix:\n", R)
66
67    # Draw Axis
68    cx = img.shape[1]//2
69    cy = img.shape[0]//2
70    size = 100
71    # X-axis pointing to right. drawn in red
72    x1 = size * R[0, 0] + cx
73    y1 = size * R[1, 0] + cy
74    # Y-axis drawn in green
75    x2 = size * R[0, 1] + cx
76    y2 = size * R[1, 1] + cy
77    # Z-axis (out of the screen) drawn in blue
78    x3 = size * R[0, 2] + cx
79    y3 = size * R[1, 2] + cy
80
81    cv2.line(img, (int(cx), int(cy)), (int(x1),int(y1)), (0,0,255), 2)
82    cv2.line(img, (int(cx), int(cy)), (int(x2),int(y2)), (0,255,0), 2)
83    cv2.line(img, (int(cx), int(cy)), (int(x3),int(y3)), (255,0,0), 2)
84
85    cv2.imshow("View", img)
86    cv2.waitKey(0)
87    cv2.destroyAllWindows()
88    print("End")

Summary

The representation of roll, pitch and yaw in xyz space depends on a perspective.
Therefore I need to be concerned about which field I am dealing with, e.g.head pose, airplane.

まぁそういう時もある。

How to draw the Euler angles in the xy plane for head pose